今回テックブログを書くにあたり、以下の記事を参考にしました。

こちらの記事では、マクドナルドのメニューを対象に組み合わせ最適化問題を扱っており、内容も非常に面白く読ませて頂きました。今回、弊社askenでも自社データを使用して食事の組み合わせ最適化問題をやってみたのでご紹介します。

はじめに

こんにちは！

askenで機械学習エンジニアとして働いているyumaです。 shoku_panという名前でTwitterをやってます。

さてみなさん、弊社ダイエットアプリ「あすけん」をご存知ですか？

www.asken.jp

あすけんでは、その日の食事内容を記録すると栄養士の未来（みき）さんからアドバイスをもらえます。点数も出るので、高得点をとることがモチベーションになっている方もいらっしゃると思います。

もちろん僕も使っています。ちなみに今年のお正月はこのような結果になりました。

32点、これはヒドい。

なにが良くなかったのか、詳しく見てみましょう。

このように、あすけんでは各栄養成分についても細かく過不足が確認できます。

左のグラフを見ると、全体的に摂取量が不足しているようですね。脂質に加えて、炭水化物や飽和脂肪酸、塩分は過剰となっていました。どれぐらい摂取すれば適正なのか、具体的な数値を確認することもできます。右の図では、例えば脂質だと基準値が36.7〜44.9gとなっています。

32点よりもいい点数をとりたい、どうせなら100点をとりたい…。

高得点をとるためには、当然のことながらバランス良く栄養をとる必要がありそうです。あすけん健康度の点数はどのように計算されているのか。調べたところ、以下のように書かれていました¹。

「食事のバランスと適度な運動が重要である」、と。わかっちゃいるけどなかなかできないんだよなぁ…。

あすけん健康度では

食事摂取カロリー
運動消費カロリー
食事バランス
PFCバランス
お菓子・アルコールの量

が評価項目になっているようです。なるほど…。

では、せっかくなので

「これら全ての評価項目を適正値にする食事の組み合わせを考えて100点とる」

ことに挑戦してみましょう！

なお、今回はあくまで食事の組み合わせだけを考えるため、「運動消費カロリー」は別途適正値をとるよう設定しています（「ジョギング20分」「筋トレ10分」など）。

さて、ここで「食事バランス」という言葉が出てきました。

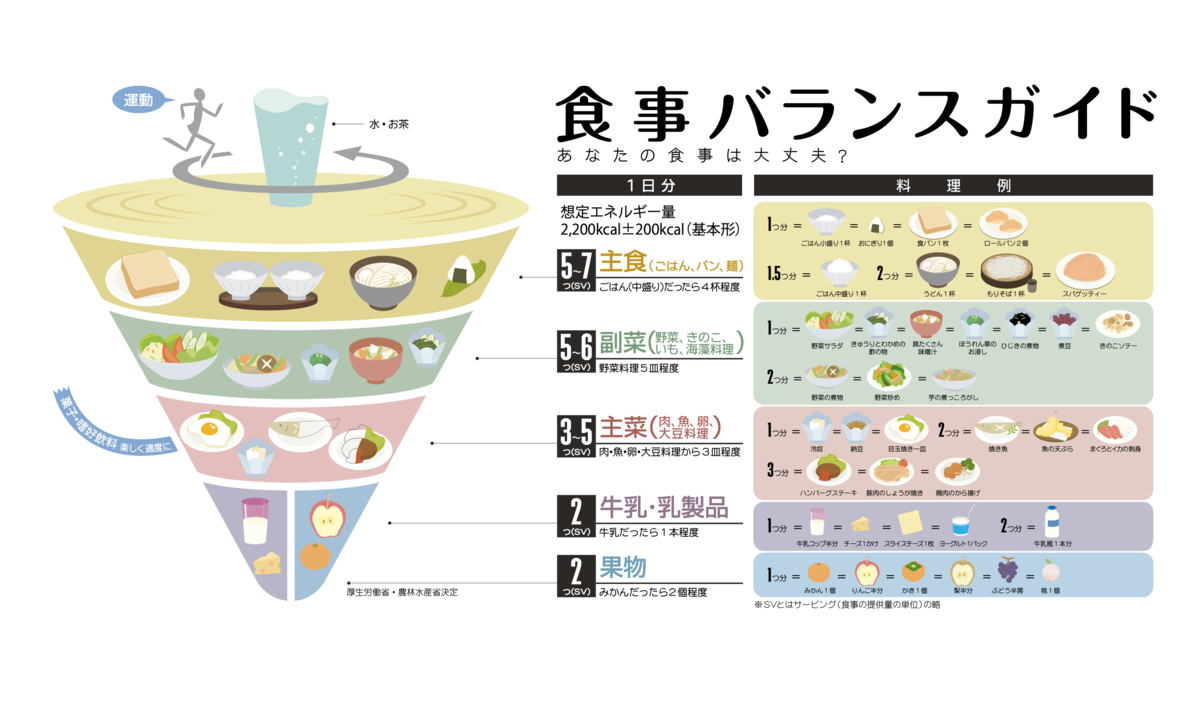
この図²によると、想定する摂取カロリーが2,200kcal±200kcalの場合、主食は5~7SVとなっています。このSVというのは食事バランスガイドの「単位」です（以下、簡単のため食事バランス自体もSVと書くことがあります）。たとえば、ご飯中盛り2杯とうどん1杯だと5（=1.5×2+2）SVとなります。食事バランスという考え方を使えば、1日の食事の組み合わせと量をおおまかに計算することができます。あすけんでは、食事バランスの過不足も教えてくれます。

32点の僕の場合、主食は適正、主菜は過剰でその他は不足していますね。お菓子・アルコールの量は適正となっていました。

ちなみにあすけんでは、食事バランスの適正値は以下のようになっていました。

要件の整理

それでは、ここまでの内容をいったんまとめます。

僕があすけんで100点をとるためには、以下の条件を満たす食事の組み合わせを考える必要があります³。

項目	小項目	条件
食事摂取カロリー（kcal）		1637〜1900
食事バランス（SV）	主食SV	3〜4
	副菜SV	5〜
	主菜SV	3〜4
	果実SV	2
	乳製品SV	2
お菓子・アルコールの量（kcal）		〜200
PFCバランス（g）	たんぱく質	144.6〜176.8
	脂質	36.7〜44.9
	炭水化物	186〜227.4

これら全ての条件を満たす食事の組み合わせを考えなければいけない…。いろいろと試行錯誤すればうまい組み合わせが見つかるとは思いますが、かなり大変そう…。

そこで今回は、複数条件を満たす食事の組み合わせを、

「与えられた制約条件の下で、ある目的関数を最大もしくは最小にする解を求める『最適化問題』」

として捉え、最適化問題の一つである線形計画問題として扱ってみました。

線形計画問題

それでは、線形計画問題の定義について確認します。

※数学が苦手な方は読み飛ばして頂いてかまいません。

線形計画問題（linear programming problem）とは、有限個の線形制約式（一次不等式や一次等式）のもとで線形関数（一次関数）を最小（あるいは最大）にする問題です。

線形計画問題は、 $A\in \mathbb{R}^{m \times n}, \boldsymbol{b}\in \mathbb{R}^{m}, \boldsymbol{c}\in \mathbb{R}^{n}$ として、 $A\boldsymbol{x}\leq \boldsymbol{b}, \boldsymbol{x}\geq\boldsymbol{0}$ （制約条件）を満たす $\boldsymbol{x}\in \mathbb{R}^{n}$ で線形関数（目的関数） $\boldsymbol{c}^{T}\boldsymbol{x}$ を最小化する問題として、

$\begin{align} \text{min}~~~~~ &\boldsymbol{c}^{T}\boldsymbol{x}\\ \text{subject to}~~~~~ &A\boldsymbol{x}\leq\boldsymbol{b}\\ &\boldsymbol{x}\geq \boldsymbol{0} \end{align}$

と書くことができます⁴。

ここで、 $\mathbb{R}$ を実数全体の集合、 $\boldsymbol{c}^{T}$ は $\boldsymbol{c}$ の転置を表します。具体的に

$A = \begin{pmatrix}a_{11} ~~a_{12} ~~\cdots ~~a_{1n}\\a_{21}~~ a_{22}~~ \cdots ~~a_{2n}\\ \vdots\\ a_{m1}~~ a_{m2}~~ \cdots ~~a_{mn}\end{pmatrix},~~~ \boldsymbol{b}=\displaystyle \left(\begin{array}{c}b_1\\ b_2\\ \vdots\\ b_m \end{array}\right),~~~ \boldsymbol{c}=\displaystyle \left(\begin{array}{c}c_1\\ c_2\\ \vdots\\ c_n \end{array}\right),~~~ \boldsymbol{x}=\displaystyle \left(\begin{array}{c}x_1\\ x_2\\ \vdots\\ x_n \end{array}\right)$

と書くことにすると

$\begin{align} \text{min}~~~~~ &c_1x_1+c_2x_2\cdots +c_nx_n\\ \text{subject to}~~~~~ \displaystyle &a_{11} x_1+a_{12}x_2\cdots +a_{1n}x_n\leq b_1\\ \displaystyle &a_{21} x_1+a_{22}x_2\cdots +a_{2n}x_n\leq b_2\\ &\vdots \\ \displaystyle &a_{m1} x_1+a_{m2}x_2\cdots +a_{mn}x_n\leq b_m\\ &x_1, x_2, \cdots ,x_n \geq 0 \end{align}$

と書くこともできます⁵。

線形計画問題を解く方法（線形計画法）としては、シンプレックス法（simplex method、単体法）というアルゴリズムが有名で、実用上も高速であることから広く用いられています。

さて、このような形にできる問題は、線形計画問題として扱うことができます。しかし、線形計画問題として扱えることと、それが解けることとは話が別です。

線形計画問題を解くことができる場合を実行可能（その解を実行可能解）、解くことができない場合を実行不能と言います。実行可能解のうち、目的関数を最適にする解を最適解といいますが、最適解は必ずしも存在するとは限りません。

以下の例で確認してみましょう。

①最適解が存在

$\begin{align} \text{min}~~~~~ &-x_1 - 2 x_2\\ \text{subject to}~~~~~ &x_1+x_2 = 1\\ &x_1, x_2 \geq 0 \end{align}$

この場合、最適解は $(x_1, x_2)=(0,1)$ となります。

②実行可能だが最適解が存在しない

$\begin{align} \text{min}~~~~~ &-x_1 - x_2\\ \text{subject to}~~~~~ &x_1-x_2 = 1\\ &x_1, x_2 \geq 0 \end{align}$

この場合、 $x_1 - x_2=1$ を満たす $x_1, x_2 \geq 0$ としていくらでも大きな値をとることができるので、実行可能ですが最適解は存在しません。

③実行不能

$\begin{align} \text{min}~~~~~ &2x_1 - 4 x_2\\ \text{subject to}~~~~~ &x_1+x_2 = -1\\ &x_1, x_2 \geq 0 \end{align}$

この場合、 $x_1+x_2 = -1$ を満たす $x_1, x_2 \geq 0$ は存在せず、実行不能となります。

定式化

※この部分も、数学が苦手な方は読み飛ばして頂いてかまいません。

線形計画問題がどういったものかがわかったところで、複数条件を満たす食事の組み合わせを線形計画問題として扱う方法を考えます。

あすけんには、膨大な食品データのデータベースがあり、各食品がどういった栄養成分をどれだけ含むかといった情報を持っています⁶。

ここで、ご飯や味噌汁などといった食品の数を $n$ コ、「食事摂取カロリー」「食事バランス」「お菓子・アルコールの量」「PFCバランス」といった項目の数を $m$ コとします⁷。そして、

食品 $j$ を選ぶ個数を $x_j (x_j=0,1,2,\cdots)$
食品 $j$ に含まれる項目 $i$ の量を $a_{ij}$
項目 $i$ の適正範囲の上限および下限を $b_i^{\rm max(min)}$

とすると、項目 $i(i=1,2,\cdots m)$ に対して許される条件は

$\displaystyle \begin{cases} a_{i1}x_1+a_{i2}x_2+\cdots a_{in}x_n \leq b_i^{\rm max}\\ a_{i1}x_1+a_{i2}x_2+\cdots a_{in}x_n \geq b_i^{\rm min}\\ x_1, x_2, \cdots ,x_n \geq 0 \end{cases}\\$

という制約条件になります。

さらに、食品 $j$ に含まれるカロリーの量を $c_{j}$ として、目的関数を

$\displaystyle c_{1}x_1+c_{2}x_2+\cdots c_{n}x_n$

とすると、

$\begin{align} \text{min}~~~~~ &c_{1}x_1+c_{2}x_2+\cdots c_{n}x_n\\ \text{subject to}~~~~~ &b_1^{\rm min} \leq a_{11}x_1+a_{12}x_2+\cdots a_{1n}x_n \leq b_1^{\rm max}\\ &b_2^{\rm min} \leq a_{21}x_1+a_{22}x_2+\cdots a_{2n}x_n \leq b_2^{\rm max}\\ &\vdots\\ &b_m^{\rm min} \leq a_{m1}x_1+a_{m2}x_2+\cdots a_{mn}x_n \leq b_m^{\rm max}\\ &x_1, x_2, \cdots ,x_n \geq 0 \end{align}$

は、

「あすけん健康度が100点でありかつ摂取カロリーを最小化する食事の組み合わせを求める」

という線形計画問題になります。

実装

複数条件を満たす食事の組み合わせを線形計画問題として扱えることがわかったところで、いよいよ実装に入ります。

今回は、言語はPython、環境はGoogle Colaboratoryを使用しました。

PuLP

Pythonで線形計画問題を扱うために、PuLPというライブラリを使用します。まずはインストールしておきましょう。

!pip install pulp

PuLPの使い方を確認するために、まずは線形計画問題の説明であげた簡単な例で動かしてみましょう。

①最適解が存在

$\begin{align} \text{min}~~~~~ &-x_1 - 2 x_2\\ \text{subject to}~~~~~ &x_1+x_2 = 1\\ &x_1, x_2 \geq 0 \end{align}$

from pulp import *

prob = LpProblem(sense=LpMinimize) # モデルの作成（最小化問題）
x1 = LpVariable('x1', lowBound=0) # 変数の作成
x2 = LpVariable('x2', lowBound=0) # 変数の作成
prob += -x1-2*x2 # 目的関数の設定
prob += x1+x2 == 1 # 制約条件の設定
prob.solve() # 解く
print(LpStatus[prob.status]) # 解の状態
print(value(x1), value(x2)) # 解
# Optimal
# 0.0 1.0

PuLPで線形計画問題を解く流れは以下です。

モデルを作成します。LpProblem(sense=LpMinimize)とすることで最小化問題のモデルprobを作成しています（最大化問題はLpMaximize）。
変数 $(x_1, x_2)$ を作成します。LpVariableに変数名（x1, x2）と最小値（lowBound=0）を与えています。さらにupBound=10などとして最大値を設定することもできます。
目的関数を設定します。目的関数は、作成したモデルprobに一次関数を追加することで設定できます。
制約条件を設定します。制約条件は、作成したモデルprobに一次不等式もしくは一次等式を追加することで設定できます。
最後にprob.solve()として問題を解きます。得られた解の状態はLpStatus[prob.status]、実際の解の値はvalue(x1), value(x2)で取得できます。

実行した結果、「最適解（Optimal）」と、最適解 $(x_1, x_2)=(0.0, 1.0)$ が確かに得られました。

「②実行可能だが最適解が存在しない」「③実行不能」についても同様に実行でき、それぞれ「最適解無し（Unbounded）」「実行不能（Infeasible）」となることが確認できます。

では実際に食品のデータに対してPuLPを使ってみましょう。

今回使用した食品データ（data.csv）は以下の内容です。

id（str）：食品のid
name（str）：食品名（ご飯や味噌汁など）
energy（float）：食品のカロリー
shushoku_sv、shusai_sv、fukusai_sv、fruits_sv、milk_sv（全てfloat）：食品の各食事バランス
protein、lipid、carbohydrate（全てfloat）：食品のPFC
alcohol、okashi_energy（全てfloat）：お菓子・アルコールの量

あらかじめ、pandasでdataframeとして用意しておきます。

import pandas as pd

df = pd.read_csv('data.csv')

また、各項目の最小値と最大値を辞書として用意しておきます。

# 各項目の最小値と最大値を設定
item_dict = {
    'energy' : {'min': 1637, 'max': 1900},
    'shushoku_sv' : {'min': 3, 'max': 4},
    'fukusai_sv' : {'min': 5, 'max': 99},
    'shusai_sv' : {'min': 3, 'max': 4},
    'fruits_sv' : {'min': 2, 'max': 2},
    'milk_sv' : {'min': 2, 'max': 2},
    'okashi_alcohol' : {'min': 0, 'max': 200},
    'protein' : {'min': 144.6, 'max': 176.8},
    'lipid' : {'min': 36.7, 'max': 44.9},
    'carbohydrate' : {'min': 186, 'max': 227.4},
}

次に関数を用意しておきます。

# 関数定義
def create_LpVariable(x, lowBound, upBound):
    """変数（LpVariable）を作成する"""
    return LpVariable(name=str(x), lowBound=lowBound, upBound=upBound, cat='Integer')

def show_result(df, lp_status):
    """結果を表示する"""
    df = df[['name', 'value'] + list(item_dict.keys())]
    df = df[df['value']>=1] # 組み合わせとして選ばれた食品のみ表示
    df = df.astype({'value': int})
    print(f'STATUS {lp_status}\n')
    for i in item_dict:
        print('{}   {:.2f}（{}〜{}）'.format(i, (df['value']*df[i]).sum(), item_dict[i]['min'], item_dict[i]['max']))
    display(df[['name', 'value', 'energy']].sort_values('value', ascending=False))

def solve_lp_problem(df, lowBound, upBound):
    """線形計画問題を設定して解く"""
    prob = LpProblem(name="asken_lp_problem", sense=LpMinimize) # モデルの作成（最小化問題）
    df['var'] = df['id'].apply(create_LpVariable, args=(lowBound, upBound)) # 変数の作成。idを変数名として作成した変数をvar列に格納している。
    prob += (df['var']*df['energy']).sum() # 目的関数の設定
    for item in item_dict: # 制約条件の設定
        prob += (df['var']*df[item]).sum() >= item_dict[item]['min']
        prob += (df['var']*df[item]).sum() <= item_dict[item]['max']
    prob.solve() # 解く
    lp_status = LpStatus[prob.status] # 解の状態
    df['value'] = [row['var'].value() for _, row in df.iterrows()] # 解
    return df, lp_status

詳細な説明は割愛しますが、dataframeの各行に対して変数を作成し、各項目の値と掛け算したものを制約条件とする部分が普通の変数での計算と勝手が若干異なります。これに関しては、変数を作成する関数create_LpVariableを別途用意し、dataframeのapplyを使うことによって、各行のidを変数名として作成した変数をvar列に格納しています。

それでは早速実行してみましょう。

lowBound = 0 # 最小値
upBound = 999 # 最大値
sample_num = 300
df_sample = df.sample(n=sample_num) # ランダムサンプリング
df_res, lp_status = solve_lp_problem(df_sample, lowBound, upBound)
show_result(df_res, lp_status)

制約条件の最小値を0、最大値は特に設けず999としています。これは、同じ食品をいくつ選んでもよい（ただし999以下）ことに相当します。また、組み合わせはデータから毎回ランダムに300個取り出すようにしています。データを絞り込むことで実行時間を短くすると同時に、様々な最適解を出してみようとしました。

場合によっては、選ばれた300個の組み合わせでは実行不能（Infeasible）となることもあり、そのときは最適解（Optimal）が出るまで実行します。1回の実行時間はおよそ1〜2秒でした。

最適解の1つはこちらです（画像の一部を加工しています）。

お腹たっぷんたっぷんになっちゃう。

20杯ぐらいで飽きちゃいそうなので、とりあえずupBound=5として同じ食品は最大でも5個までとしてみました。5個までならなんとかいけるのでは…？

最大値を5としてみた結果は以下です。

これは先程の結果に比べると現実的ではないでしょうか？！

うーん、刻みのり食べるのに焼きのりも食べるんですね

はなっこりー…？

ja.wikipedia.org

「はなな（花菜）」と「ブロッコリー」で「はなっこりー」。山口県では特に有名だそうです。甘みもあり、ホウレンソウ並みのビタミンC、食物繊維も豊富だそう。なるほど、知らなかった…。

ランダムサンプリングしているので、実行する度に結果が異なります。他の最適解も見てみましょう。

さて、それではいよいよこの食事の組み合わせをあすけんに登録してみます。

結果は…

100点、それはそう。

シミュレーションだけじゃダメですね。実際に、ちゃんと食べるまでがあすけんです。

まとめ

今回、あすけんで100点をとる食事の組み合わせを考えました。複数条件を満たす食事の組み合わせを探す問題を、最適化問題の一つである線形計画問題として扱いました。

線形計画問題は、PythonではPuLPを使って実装することができます。

無事「100点をとる」という目標は達成できたのですが、結果を確認すると以下の課題が考えられました。

朝昼晩に分けて考える
あすけんでは、1食だけでなく朝昼晩の3食すべてを記録することで点数を見ることができます。今回は結果を適当に3食にわけて登録しましたが、実際には1食ごとに食事の組み合わせを考える必要があります。
妥当な組み合わせを考える
たとえば「ご飯・味噌汁・焼き魚」「パン・ヨーグルト・野菜ジュース」はよくある組み合わせだと思いますが、「パン・焼き魚・シュウマイ」などはあまり見ない組み合わせかと思います。
手に入れやすいものに絞る
あすけんのデータベースには、一般的な食品からレアな食品まで多岐にわたる食品のデータが登録されています。提示された食品が自分にとって入手しづらいものであればあまり意味がありません（近いもので代用するという手はありますが）。広く一般的な食品、あるいはその人にとって手に入れやすいものに限定して組み合わせを提示する必要性があるかもしれません。

みなさんも、あすけんを使ってオリジナルの100点レシピをつくってみませんか？

バランスのよい食事と適度な運動で、健康な毎日を過ごしてくださいね

お知らせ

askenでは、一緒に働いてくれるエンジニアを募集しています！

www.wantedly.com

主な参考資料

3食記録後に表示される、アドバイス画面の摂取栄養素グラフ「判定基準」ボタンから確認できます。↩
https://www.maff.go.jp/j/balance_guide/↩
食事摂取カロリーは、グラフでは「1637〜2037(kcal)」が適正範囲となっていますが、SVの適正範囲（食事摂取カロリーによって変わる）を固定して扱いやすくするため、最大値を1900(kcal)としています。↩
「subject to」は「〜という条件のもとで」という意味です。↩
実際には、線形計画問題の基準系（canonical form）は、目的関数を最大化する問題です。しかし、目的関数を最大化する問題は、 $-1$ 倍した目的関数を最小化する問題と捉えることができます。また、上記基準系の制約条件はすべて「 $\leq$ 」の向きになっていますが、「 $\geq$ 」のものがあったとしても両辺に $-1$ をかけることで向きを揃えることができます。さらに、制約条件に等式があった場合でも、非負の実数を新たに加えることで不等式にすることができます。今回は簡単のため、上記の形式を線形計画問題として扱うことにします。↩
今回、市販食品のデータは対象外としています。↩
実際には今 $m=10$ ですが、一般的な形で書いています。↩